Many apps with client-side encryption that use passwords derive both encryption and server authentication keys from them.

One such example is Bitwarden, a cross-platform password manager. It uses PBKDF2-HMAC-SHA-256 with 100,000 rounds to derive an encryption key from a user’s master password, and an additional 1-round PBKDF2 to derive a server authentication key from that key. Bitwarden additionally hashes the authentication key on the server with 100,000-iteration PBKDF2 “for a total of 200,001 iterations by default”. In this post I’ll show you that these additional iterations for the server-side hashing are useless if the database is leaked, and the actual strength of the hashing is only as good as the client-side PBKDF2 iterations plus one HKDF and one HMAC. I will also show you how to fix this.

(Note that this post is from 2020 and discusses Bitwarden’s authentication scheme as it was at that time. Since then, Bitwarden were working on improving it.)

Since Bitwarden doesn’t have publicly available documentation (which is unfortunate for an open source project), I rely on documentation provided by Joshua Stein who did a great job of reverse-engineering the protocol for his Bitwarden-compatible server written in Ruby.

On the client side, PBKDF2 is used with a user’s password and email to derive a master key. (The email address is used a salt. I’m not a big fan of such salting, but we won’t discuss it today). This master key is then used to encrypt a randomly generated 64-byte key (which encrypts user’s data) — we’ll refer to the result as a protected key. The master key is then again put through PBKDF2 (with one iteration this time), to derive a master password hash, which is used to authenticate with the server. The server runs the master password hash through PBKDF2 and stores the result in order to authenticate the user. It also stores the protected key.

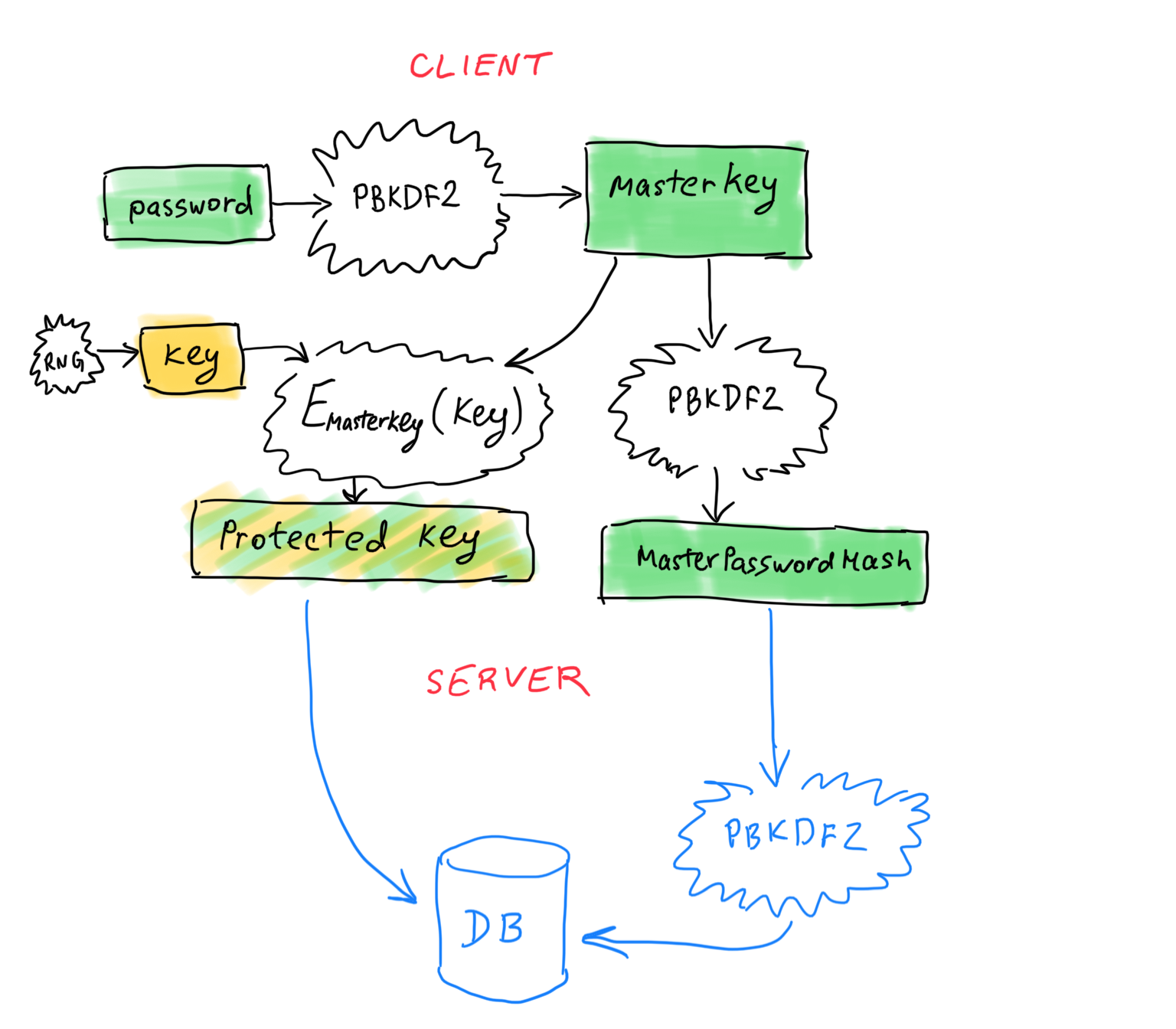
To authenticate a user, the server receives the master password hash, hashes it with PBKDF2, and compares the result with the stored hash. If they are equal, authentication is successful, and the server sends the protected key to the client, which will decrypt it to get the encryption key.

The additional hashing on the server has two purposes: to prevent attackers that get access to the stored hash from authenticating with the server (they need to undo the last hashing for that, which is only possible with a dictionary attack), and to improve resistance to dictionary attacks by adding a random salt and more rounds to the client-side hashed password.

The last part does not work well in the described scheme. Have you noticed that the protected key is the random key encrypted with the master key (which is derived from the password)?

protectedKey = AES-CBC(masterKey, key)

That random key is used to encrypt and authenticate user data, such as login information, passwords, and other information that the password manager deals with. One part of the key (let’s call it key1) is used for encryption with AES-CBC, another part (key2) is used with HMAC to authenticate the ciphertext:

encryptedData = AES-CBC(key1, data)
encryptedAndAuthenticatedData = HMAC(key2, encryptedData)

(I’m skipping initialization vectors and other details for clarity.)

The result, encryptedAndAuthenticatedData, is stored on the server. To decrypt data, Bitwarden client needs the user’s password, from which it derives the master key with PBKDF2, then decrypts the key from the protectedKey it fetched from the server, and then uses that key to decrypt data.

If Bitwarden’s server database is leaked, the attackers do not need to run dictionary attacks on the master password hash, which has additional PBKDF2 rounds. Instead, they can run the attack as follows:

1. Derive master key: masterKey = PKBDF2(passwordGuess)
2. Decrypt protectedKey (AES-CBC) to extract the HMAC key (key2).
3. Verify the HMAC key against a piece of user’s encrypted data.
4. If it verifies, the password guess it correct; otherwise try other guesses.

(Update (January 2023): actually, we don’t even need AES decryption and verification, since it uses Encrypt-then-MAC — we only need HMAC, plus HKDF for deriving the MAC key.)

As you can see, instead of PBKDF2(PBKDF2(passwordGuess, 100,001), 100,000), which is 200,001 iterations, attackers can run HMAC(AES-CBC(PBKDF2(passwordGuess, 100,000))) HMAC(HKDF(PBKDF2(passwordGuess, 100,000))), which is 100,000 iterations of PBKDF2, two AES blocks (they only need 32 bytes from protectedKey) HKDF, and one HMAC. This attack is not necessary cheaper in Bitwarden’s case than the standard one on PBKDF2, since it includes the cost for an additional circuit for AES and passing around a bit more data compared to just running an additional PBKDF2-HMAC-SHA-256 with 100,000 iterations. However, when this authentication scheme is used with a better server-side password hashing function, the attack cost can be significantly reduced.

The fix is simple. But let’s first generalize our authentication/encryption scheme:

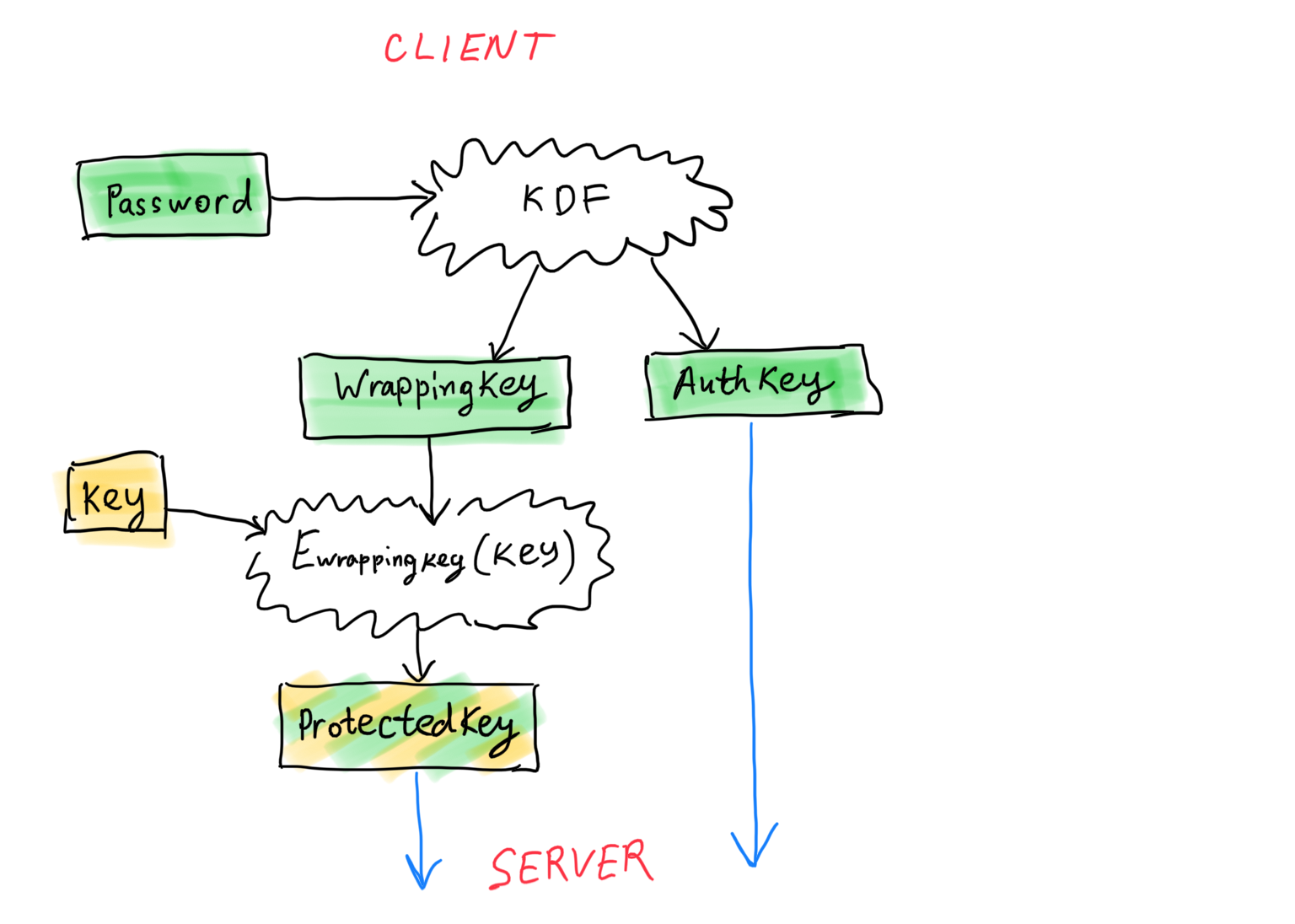
Derive two keys from a password using a password-based key derivation function: wrappingKey and authKey. The first one is used to encrypt random key material to get protectedKey, which is then sent to the server during the registration or re-keying, the second one is sent to the server for authentication.

In Bitwarden’s case, authKey will be again hashed and stored, while protectedKey will be stored as is (allowing attackers to use it to verify password guesses without additional hashing).

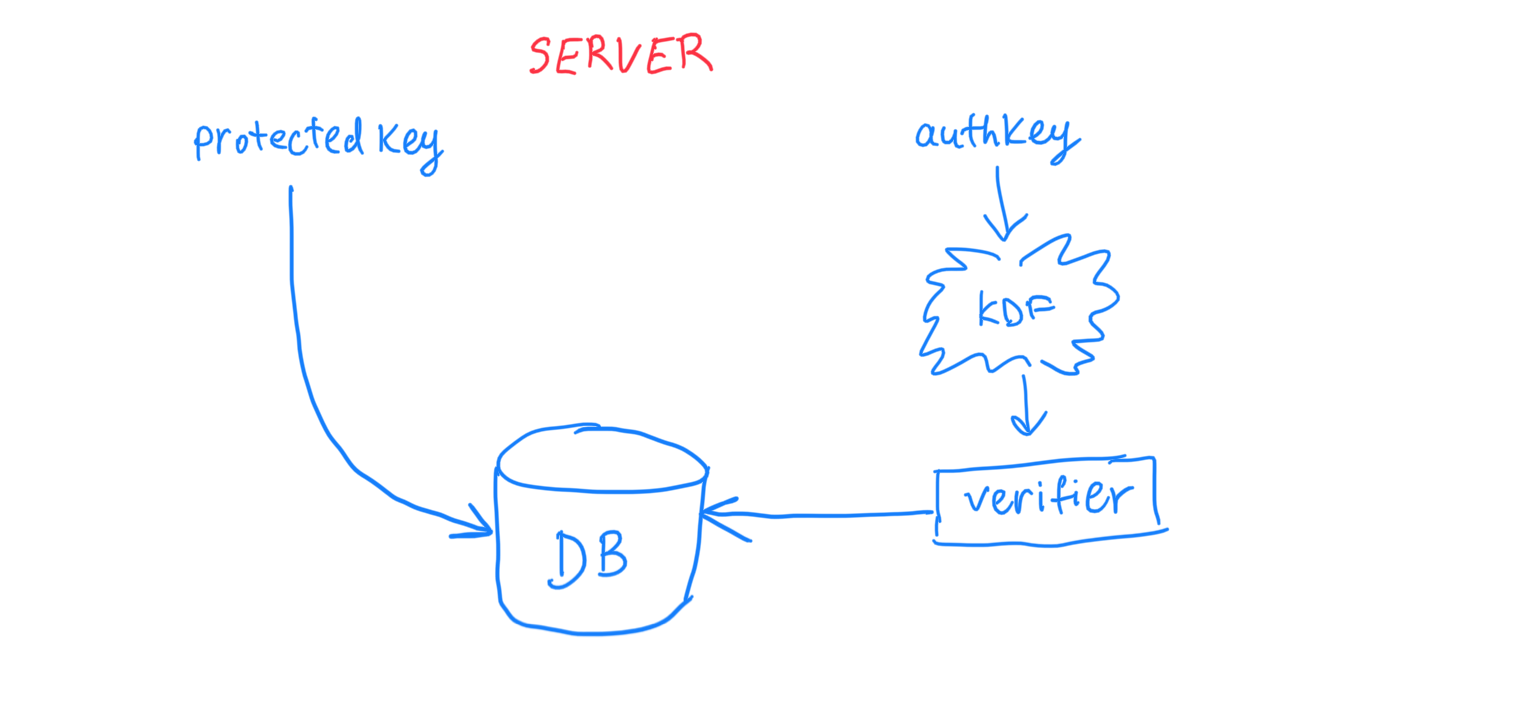
The improvement that I propose on the server side looks like this:

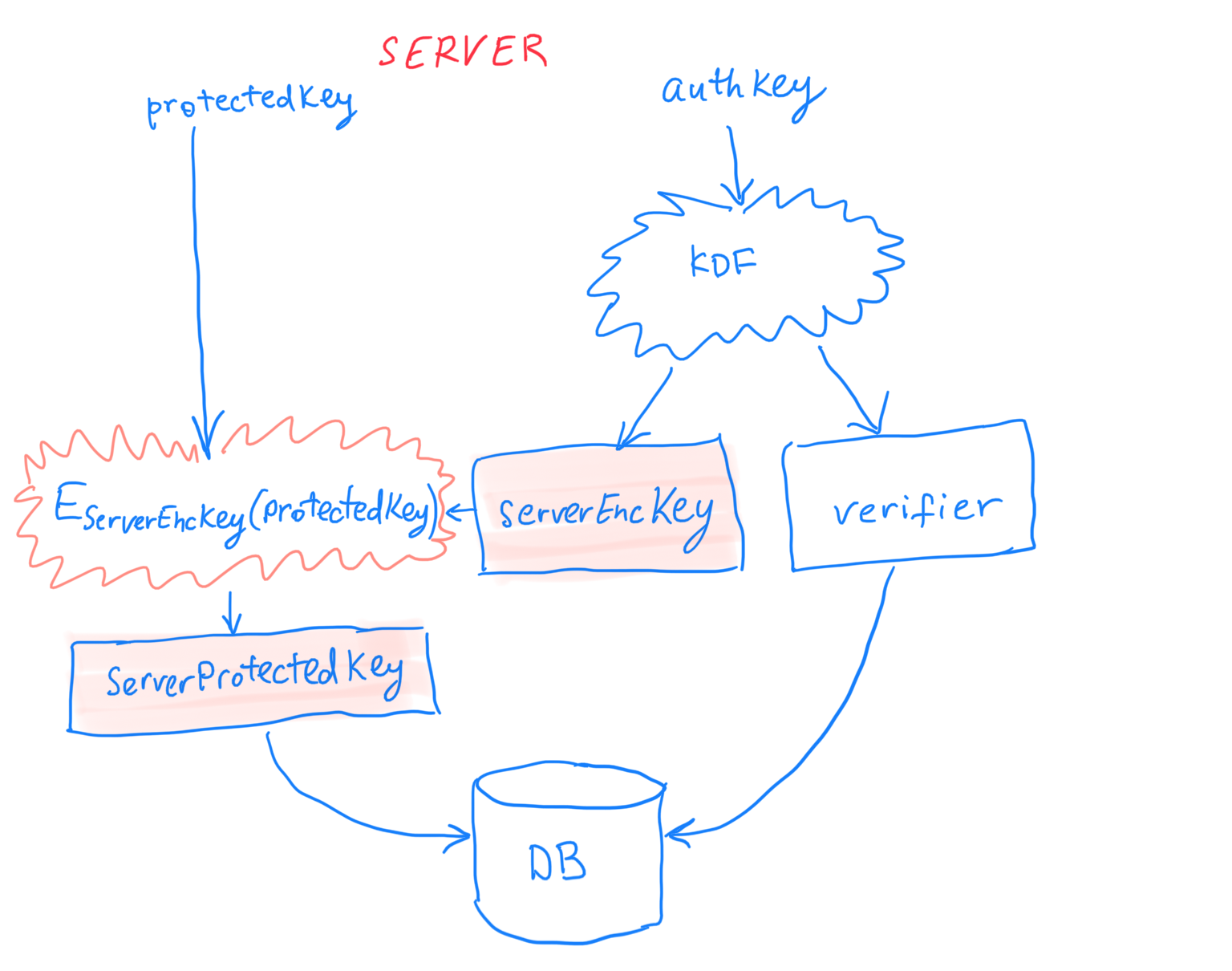
1. Instead of deriving one key (aka hash, aka verifier) with the password hashing function, derive two keys: serverEncKey and verifier. (The verifier has the same purpose as in the original scheme.) (Note: don’t use the password hashing function twice! Instead, with a modern password hashing function derive a 64-byte output and split it into two 32-byte keys, or if you’re stuck with PBKDF2, use HKDF to derive two different keys from a single 32-byte output of PBKDF2).

2. Encrypt protectedKey received from the client with serverEncKey and store the result of this encryption (serverProtectedKey) instead of protectedKey.

That’s it. When a user logs in, perform the same key derivation, and if verifier is correct, decrypt serverProtectedKey to get the original protectedKey and send it to the client. (In fact, if we use authenticated encryption, we can just use the fact that serverProtectedKey is successfully decrypted to ensure that the user entered the correct password and not store the verifier, but I like the additional measure in case the authenticated encryption turns out to have side-channel or other vulnerabilities.)

Why does it work? In the original scheme, an adversary that has a leaked database can run password guessing attacks against the verifier, which requires an additional KDF, or against the protectedKey (and in case of Bitwarden, an additional piece of user’s encrypted data, since the attacker cannot verify whether the decryption of the key was successful), which is easier. In the new scheme, the attacker would have to run the same KDF that is used on the server in any case, whether they wanted to verify guesses against verifier or serverProtectedKey. Thus, we successfully added additional protection against dictionary attacks on the server side.